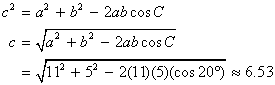MATEMÁTICAS DE DÉCIMO GRADO
ÁNGULOS
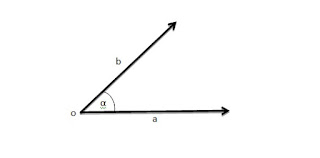
Un ángulo es la unión de dos rayos o semirrectas con el mismo origen, a las semirrectas se le denomina lados y al origen se le llama vértice
Según esta definición el orden en que se encuentra los lados del ángulo es indiferente, sin embargo en el estudio de la antigua geometría es importante tener en cuenta el lado del ángulo que se nombra primero.
Un ángulo es positivo cuando va en contra de la manecilla del reloj y es negativo cuando va a favor de la manecilla, considerado así un ángulo se llama orientados. Los ángulos también se pueden notar por letras griegas.
β- Beta
θ- Teta
Ángulos en el plano cartesiano
Un ángulo α se considera que está en posición canónica o normal si su vértice coincide con el origen ya ademas su lado inicial es el positivo de x.
Cuando un ángulo se encuentra en posición normal el lado final indica el cuadrante al cual pertenece dicho ángulo.
Dos ángulos en posición normal pueden tener el mismo lado final en este caso se dice que los ángulos son determinantes.
MEDICIÓN DE ÁNGULOS
Los ángulos se miden en grados y radianes, el grado es la medida de los ángulos en el sistema sexagecimal y el radian es la medida de los ángulos ciclito.
MEDIDAS DE ÁNGULOS EN EL SISTEMA SEXAGECIMAL
Un ángulo generado por la rotación del lado final en una vuelta mide 360°. El grado sexagecimal se define como:
1°:
1°= 60´
1´= 60"
Un ángulo expresado en el sistema decimal se puede representar en el sistema sexagecimal de las siguientes maneras:
Ejemplo:
35,225° ⇒ 35°
0.225* 60= 13,5 ⇒ 13´
0,5*60= 30"
35,225°= 35° 13´ 30"
MEDIDAS DE ÁNGULOS EN EL SISTEMA CÍCLICO
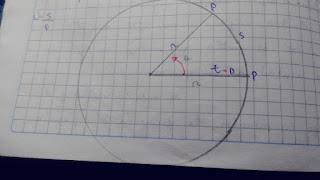
Sobre una circunferencia un ángulo central α y se determina un alto, arco AB se dice que la medida de un ángulo α es un radian si la longitud del arco AB que le corresponde es igual al radio de la circunferencia.
Un radian es la medida de un ángulo central de una circunferencia cuyo alto mide igual que un radio.
EQUIVALENCIAS ENTRE EL SISTEMA SEXAGECIMAL Y EL CÍCLICO
Como el perímetro de toda circunferencia es p= 2π r donde π es 3,1415 y r el radio de la circunferencia, la cantidad de veces que está el radio r de una circunferencia de su perímetro. Esta dado por el cociente:

Esto quiere decir que un ángulo completo cuya medida es de 360° equivale a 2π rad
Para determinar la equivalencia de un grado en radaianes se realiza los siguientes pasos 360°= 2π rad
Para determinar la equivalencia de un radian en grados se tiene que:
En la siguiente figura se muestra algunas equivalencias entre grados y radianes
Ejemplo:
LONGITUD DE ARCO
Es posible determinar la medida de un arco si es descrito sobre una circunferencia a partir del siguiente razonamiento.
Como un ángulo de 2π r determinar la medida de cualquier circunferencia sin importar que radio tenga.
A partir del gráfico se puede plantear la siguiente proporción:
VELOCIDAD ANGULAR Y LINEAL
Velocidad angular
Cuando un objeto gira, su rapidez depende al ángulo que barre y el tiempo empleado en barrer dicho ángulo por ejemplo en la siguiente figura un ángulo θ en un tiempo t, todos sus radios barren el mismo ángulo en dicho tiempo.
Si un objeto gira ángulos iguales en tiempos iguales; se define velocidad angular w= θ/t
la velocidad angular se mide rad/s o rad/h
El numero de vueltas que realiza un objeto en una unidad de tiempo se mide en vueltas y el tiempo en minutos, la frecuencia se expresa en (r.p.m)
Ejemplo:
Determinar la velocidad angular de la polea de un motor que gira a 1000 revoluciones por minuto, el ángulo que gira en un minuto es.
Velocidad lineal
Si un objeto gira ángulos iguales en tiempos iguales y un punto p describe un arco de longitud s en un tiempo t, se define la velocidad lineal como
La velocidad lineal se expresa en m/s o km/h
Ejemplo:
Con respecto al movimiento de la tierra alrededor de su propio eje, pero para un punto del ecuador terrestre determinar:
a- Velocidad angular
b- Velocidad lineal
Ejercicio:
La tierra efectúa un giro completo sobre su eje 24 horas
¿Cuanto tiempo le toma realizar un giro de 300°?
TRIÁNGULOS
El triángulo es un polígono de
tres lados que da origen a tres vértices y tres ángulos internos. Es la figura
más simple, después de la recta en la geometría. Como norma general un
triángulo se representa con tres letras mayúsculas de los vértices (ABC).
De acuerdo a la longitud de sus
lados, un triángulo pude clasificarse en equilátero, donde los tres lados del
triángulo son iguales; en isósceles, el triángulo tiene dos lados iguales y uno
desigual, y en escaleno, donde el triángulo tiene los tres lados desiguales.
También se pueden clasificar
según la medida de sus ángulos, puede ser un acutángulo, donde los tres ángulos
son agudos; es decir, ángulos menores que 90°. Si un triángulo presenta un
ángulo recto o ángulo de 90° se dice que es rectángulo, y si presenta a uno de
los tres ángulos como obtuso; es decir, un ángulo mayor que 90° se considera
como obtusángulo.
Los triángulos se clasifican de acuerdo a la medida de sus lados en:
Equilateros: es aquel que tiene sus lados congruentes
Isósceles: es aquel que tiene dos lados congruentes
Escaleno: es aquel que tiene sus lados de distintas medidas
Propiedades de los ángulos
De acuerdo con la medida de sus ángulos los triángulos cumplen las siguientes propiedades:
Primera propiedad
La suma de los ángulos de todos los triángulos es igual a 180°
Segunda propiedad
Todo triángulo equilatero es equiángulo
Cuarta propiedad
Si dos ángulos de un triangulo son congruentes entonces los lados opuestos a estos ángulos son congruentes.
Teorema de Pitágoras
| El Teorema de Pitágoras es una relación entre los lados de triángulos rectángulos. Un triángulo rectángulo es el que tiene un ángulo recto, esto es, un ángulo de 90º.
El teorema de Pitágoras expresa una relación entre los cuadrados de las medidas de los lados de un triángulo rectángulo.
a2 , b2, c2 son las áreas de cuadrados de lados a, b, c respectivamente.
Ejercicio
Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm
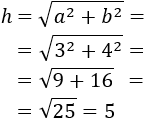
TRIGONOMETRÍA
La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'
En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas globales de navegación por satélites.
Definición de los funciones trigonométricas de un ángulo en posición normal
Si θ es un ángulo en posición normal y P (x,y) es cualquier punto contenido en el lado final diferente o (o,o) se cumple OP=
Se definen las funciones trigonométricas para el angulo θ de la siguiente manera:
Funciones trigonométricas de un ángulo en posición normal
Llamado también ángulo en posición crónica o estándar; es aquel ángulo trigonométrico cuya vértice coincide con el origen del sistema cartesiano su lado inicial coincide con el semieje positivo de y su lado se ubicará en cualquier región del plano siendo el que indique a que cuadrante pertenece dicho ángulo.
Definición de las razones trigonométricas de un ángulo en posición normal
|
Para definir o hallar las R.T de un ángulo en posición normal; se debe conocer un punto perteneciente a su lado final.
En el gráfico; para "a"; tendremos:
Por ejemplo:
Se debe notar que ahora los R.T pueden tener signo negativo; dependiendo del cuadrante en el que se ubique el ángulo considerado.
Signo de las funciones trigonométricas de un ángulo en posición normal
Para determinar el signo de las funciones trigonométricas se debe analizar el comportamiento de r, y, x.
Si θ es un ángulo en posición normal y p es un punto sobre el lado final de θ diferente del origen (0,0) se tiene que
siempre es positivo.
x y y varían dependiendo el cuadrante en donde se encuentre por lo tanto el signo del valor de la función trigonométrica para cada ángulo depende de los signos de x y y.
En la siguiente tabla se presentan los signos de las funciones de un ángulo en posición normal para los diferentes cuadrantes en que pueda estar ubicado el lado final
Ejemplo:
Funciones trigonométricas de ángulos cuadrantes
Hasta el momento se han estudiado los ángulos cuyo lado final se encuentra en uno de los 4 cuadrantes. Ahora es importante estudiar los ángulos cuyo lado final coincide con alguno de los semiejes del plano cartesiano.
Los ángulos en posición normal cuyo lado final coincide con algunos semiejes del plano cartesiano se les llama ángulos cuadrantes.
En la siguiente figura se muestra los ángulos cuadrantes de 90°, 180°, 560°, -180° y -270°
Para determinar las funciones trigonométricas de los ángulos cuadrantes se considera que sobre su lado final se encuentran algunos de los puntos.
(0,r) (-r,0) (0,-r) ((r,0) ; r>0
En el siguiente cuadro se presentan los valores de las funciones trigonométricas para los ángulos mayores o iguales de 90° y menores o iguales de 360°
Circunferencia Unitaria
El estudio de las funciones trigonométricas requiere el análisis de sus comportamientos y de la identificación de su dominio y de su rango.
La circunferencia unitaria es aquella que tiene como centro el origen del plano cartesiano y de radio la unidad.
En la figura anterior se muestra la circunferencia unitaria que contiene al punto p (x,y) al aplicar el teorema de Pitágoras se obtiene que para todos los puntos p (x,y) se cumple que:
Si θ es un ángulo en posición normal cuya medida es t rad, la medida del arco 3 subtendido por dicho ángulo en la circunferencia unitaria se obtiene mediante.
Por lo tanto en la circunferencia unitaria de t rad subtiende un arco de t unidades
Funciones trigonométricas definidas en una circunferencia unitaria
Si t es la medida de un arco descrito en la circunferencia unitaria con extremos en los puntos 81,0) y p (x,y) se tiene que:
Dominio y rango de una función
El dominio de una función f (x) es el conjunto de todos los valores que f toma.( en gramática probablemente le llame al dominio conjunto de reemplazo y al rango el conjunto de todos los valores que f toma.( En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. Quizá también estos han sido llamados la entrada y salida de la función.
Ejemplo 1:
Considera la función mostrada en el diagrama
El rango es el conjunto (1,3,4) 2 no está en el rango ya que no hay letra en el dominio que se enlace con el 2.
Trigonométria analítica
Las expresiones algebraicas se utilizan variables constantes, cuyos valores pertenecen a los números reales en este caso aplicaremos algunos procedimientos utilizados en álgebra a expresiones que involucran funciones trigonométricas.
OPERACIONES ALGEBRAICAS CON FUNCIONES
El estudio de las expresiones que
involucran las funciones trigonométricas se sumaran la suma, la resta, la
multiplicación y la división de estas expresiones.
SUMA Y RESTA DE EXPRESIONES
Para
resolver suma y resta de expresiones que involucran las funciones
trigonométricas se deben agrupar y reducir los términos semejantes.
Ejemplo:
MULTIPLICACIÓN DE EXPRESIONES TRIGONOMÉTRICAS
Para
multiplicar expresiones que involucran funciones trigonométricas, se aplican
las propiedades de la potenciación y la propiedad distributiva de la
multiplicación con respecto a la adicción o sustracción.
Ejemplo:
DIVISIÓN DE EXPRESIONES
FACTORIZACIÓN
Es
posible factorizar expresiones que involucran funciones trigonométricas
mediante los mismos métodos que se utilizan en la factorización de polinomios.
FACTOR
En
este caso es necesario identificar un factor que aparezca en todos los términos
de la expresión y aplicar la propiedad distributiva.
X
(Y + Z) = Xy + Xz
X
(Y – Z) = Xy + Xz
Ø 12 + 24 6
– 15
3*4 + 4*6 3*2
– 3*5
4(3 + 6) 3(2
– 5)
Ejemplo:
5tan22x – 25
tan2x
5*1 tan2x * tan2x -
5*5tanx
5*tan2x( tan 2x – 5)
FACTOR COMÚN POR AGRUPACIÓN
En este caso se separa la
expresión en 2 o más partes iguales. En cada una de ellas se identifica el
factor común y se aplica la propiedad distributiva, así como muestra la imagen.
DIFERENCIA DE CUADRADOS
La diferencia de cuadrados
de dos expresiones que involucran funciones trigonométricas es igual a la suma
por la diferencia de las expresiones.
Ejemplo:
SIMPLIFICACIÓN
Para simplificar una
fracción en la que el denominador y el numerador son producto de funciones
trigonométricas se aplica la propiedad de cocientes de potencias e igual base.
IDENTIDAD
Una identidad es una
igualdad entre dos expresiones que es verdadera para todos los valores de las
variables que se involucran.
Una identidad que involucra
funciones trigonométricas se denomina identidad trigonométrica.
IDENTIDADES FUNDAMENTALES
Se llaman identidades
fundamentales a las que se deducen directamente de las definiciones, estas
identidades se utilizan para transformar unas expresiones en otras lo cual
permite comprobar otras identidades y resolver ecuaciones que involucran
funciones trigonométricas
DEMOSTRACION DE UNA
IDENTIDAD
El método de demostración de una identidad consiste en demostrar que uno de los miembros de una igualdad es igual al otro para ello se sugiere los siguientes pasos:
- Transformar el miembro más complejo de la igualdad en el miembro más simple haciendo uso de las identidades fundamentales.
- De ser posible expresar las funciones trigonométricas que aparecen en la igualdad en término de la función seno y coseno
- Realizar las operaciones algebraicas para simplificar las expresiones
LEY DEL SENO
La
ley del seno es una relación que existe entre los lados y ángulos de triángulos
oblicuángulos. En todo triangulo, el seno de los ángulos y la medida de los
lados respectivamente opuestos o dichos ángulos son directamente proporcionales.
Para
poder usar esta ley se deben conocer dos ángulos y un lado (LAA o ALA) o
también 2 lados y un ángulo (LLA)
Ejemplo:
Resolver el triángulo ∆ABC con A =
55°, B = 41° y a = 4,5m.
Encontrar el ángulo y los lados faltantes.
El tercer ángulo equivale a:
A + B + C = 180°
55° + 41° + C = 180°
C = 180° - 96°
C = 84°
La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.
La ley de los cosenos establece:
c 2 = a 2 + b 2 – 2 ab cos C .
Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como
b 2 = a 2 + c 2 – 2 ac cos B or
a 2 = b 2 + c 2 – 2 bc cos A .
Ejemplo 1: Dos lados y el ángulo incluído-LAL
Dado a = 11, b = 5 y C = 20°. Encuentre el lado y ángulos faltantes.
Para encontrar los ángulos faltantes, ahora es más fácil usar la ley de los senos.
GEOMETRÍA ANALÍTICA
La geometría
analítica es una rama de las matemáticas que estudia con profundidad las
figuras sus distancias, sus áreas, puntos de intersección, ángulos de
inclinación, puntos de división, volúmenes, etc. Es un estudio más profundo para
saber con detalle todos los datos que tienen las figuras geométricas.
Creditos:
Geovanny Muñoz
Stivenson Fontanilla
Kevin Melendez
Colegio: Institución Educativa Fco José de Caldas
Soledad,Atlántico,Colombia